PROBLEMS AND SOLUTIONS 2

REPRODUCIBILITY
The touchstone of a quantitative science is an ability to reproduce results.
Biology – operating as a 50% science – struggles with the reproducible problem .
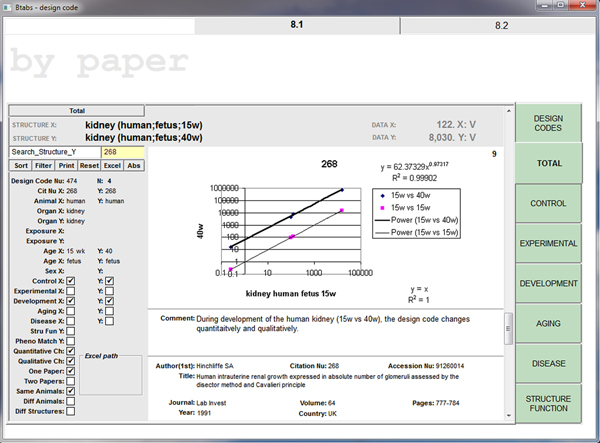
REPRODUCIBILITY - LOCAL - POSTMORTEM
Stereological data – collected postmortem – display such a capability locally (within a given paper), but…
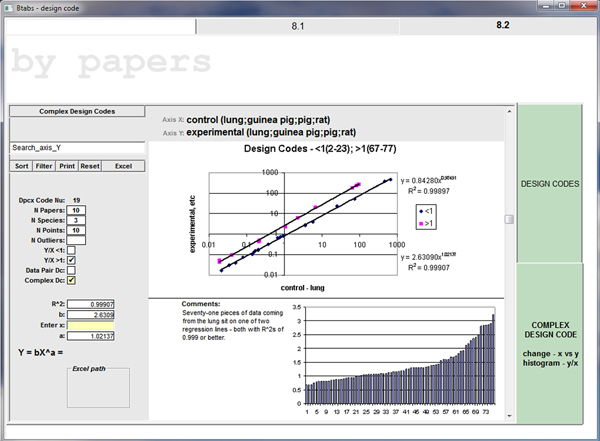
REPRODUCIBILITY - GLOBAL - POSTMORTEM
…not often globally (between papers) for the same species.
REPRODUCIBILITY - GLOBAL - LIVING
A very different outcome exists for data collected from living subjects under the auspices of complexity theory. Now reproducibility becomes commonplace – both locally and globally in the same species.

DISTORTIONS - TEST
When biological data sets fail to display global reproducibility, they most likely carry distortions (biases) produced by our experimental methods.
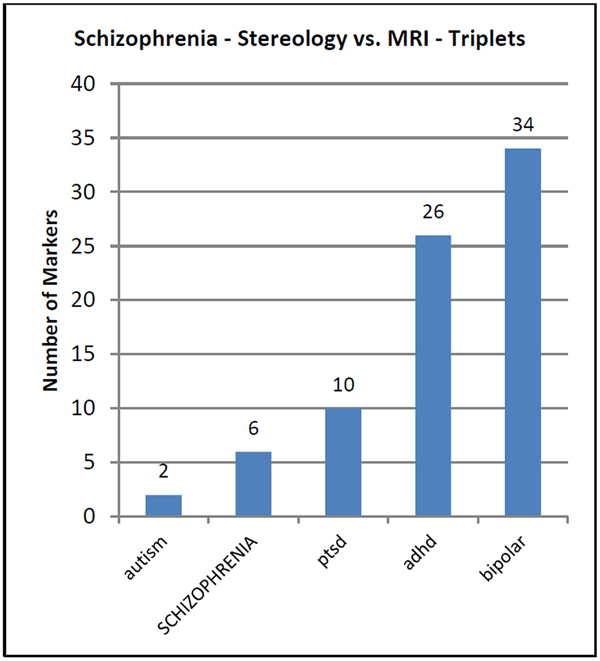
DISTORTIONS VS GOLD STANDARDS
We can test this idea by using mathematical markers for schizophrenia coming from living (MRI) and postmortem (stereology) subjects.
Using the MRI data as standards, can we diagnose patients correctly using data collected postmortem (stereology)?
No, such a test misses the correct diagnosis (SCHIZOPHRENIA) by a wide margin.
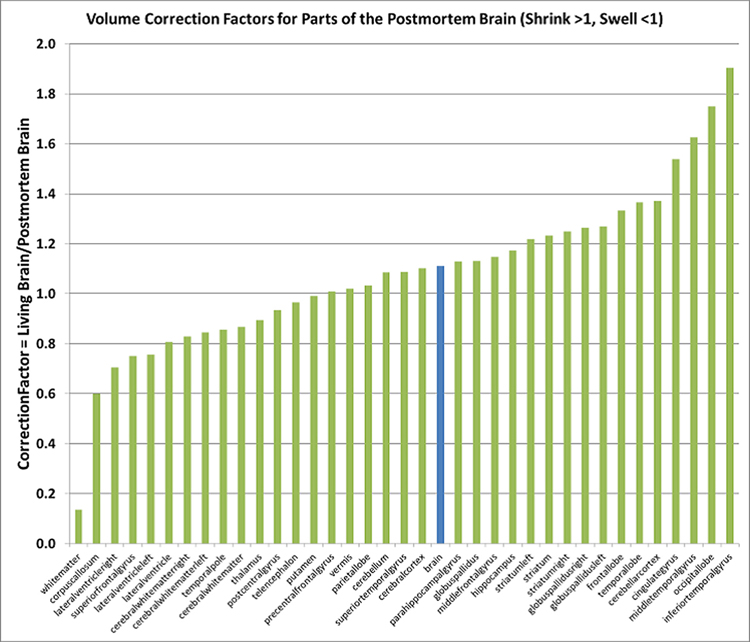
DISTORTIONS - ARE HIGHLY VARIABLE
The postmortem data carry volume distortions, including increases (swelling) and decreases (shrinkage).
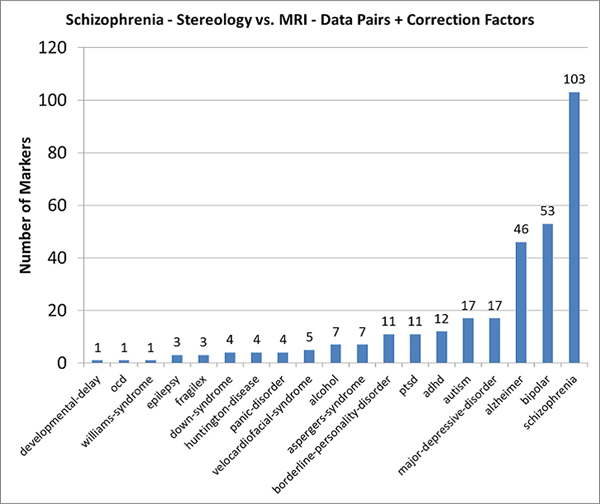
DISTORTIONS - UNDER CONTROL
Once corrections are applied, however, the postmortem markers deliver the correct diagnosis.

DISORDERS OF THE BRAIN
Disorders of the human brain affect many of the same parts.
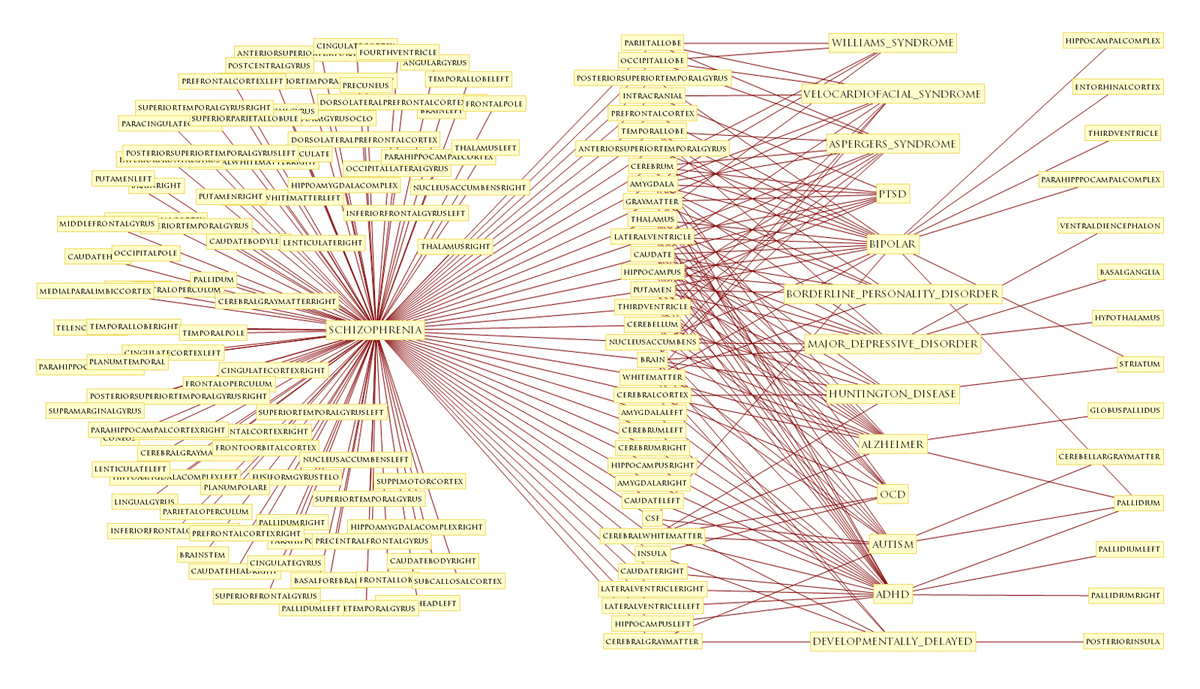
DISORDERS OF THE BRAIN - QUALITATIVE PATTERNS
Schizophrenia, for example, shares many of its parts with a host of other disorders.
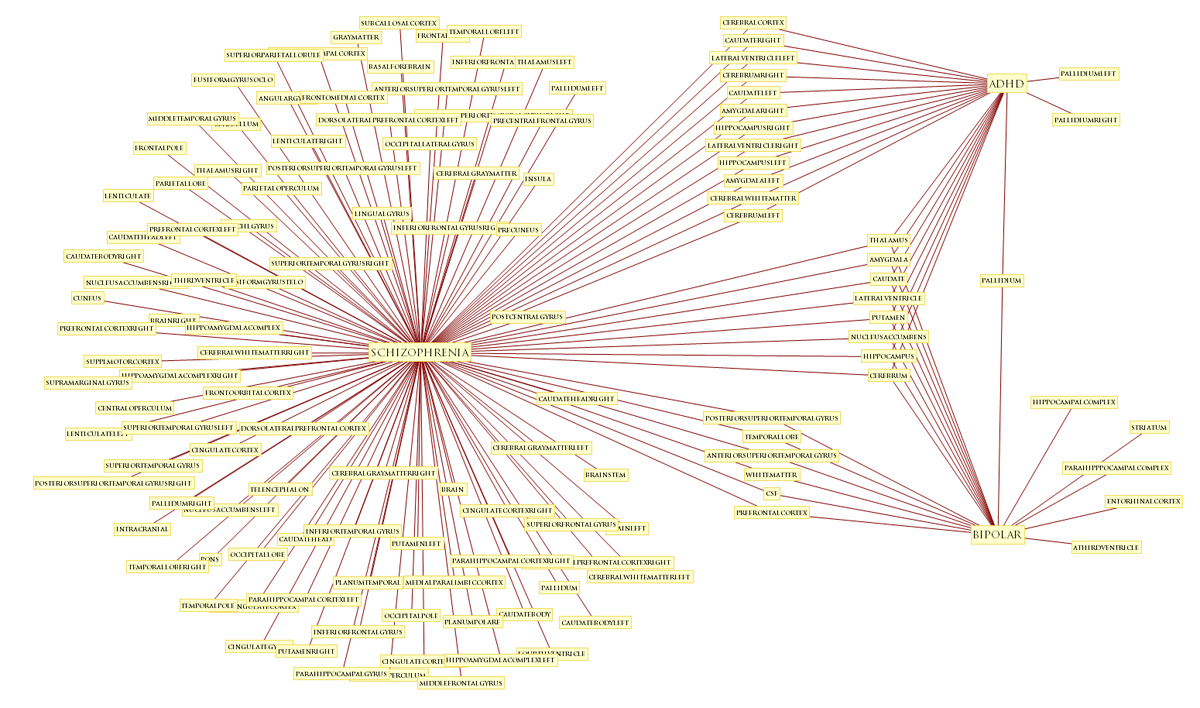
DISORDERS OF THE BRAIN - QUALITATIVE PATTERNS
In fact, the tendency of disorders to share parts is a distinct feature of the disease process.
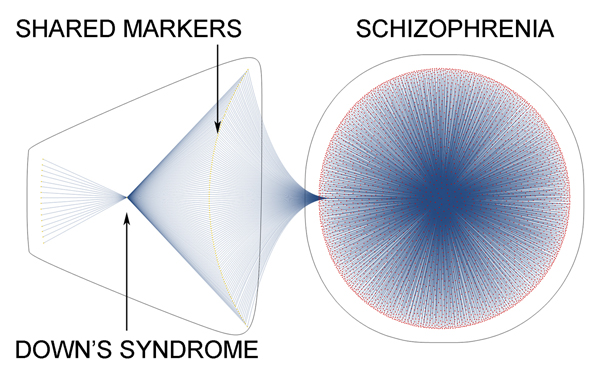
DISORDERS OF THE BRAIN - QUANTITATIVE PATTERNS
Different disorders often share exactly the same mathematical markers.
Notice that Down’s syndrome shares most of its markers with schizophrenia.

DISORDERS OF THE BRAIN - QUANTITATIVE PATTERNS
By replacing the dots with mathematical markers and disorders, we can see the quantitative relationship of one phenotype (Down’s syndrome) to another (schizophrenia).

COMMUNITIES
Disorders of the human brain form communities of shared markers.
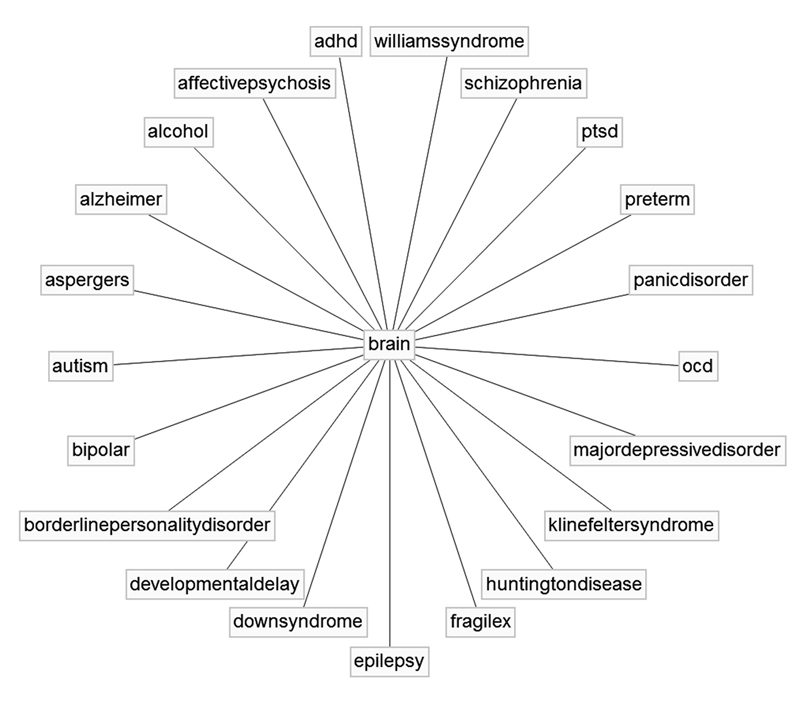
IDENTIFY THE DATA SET
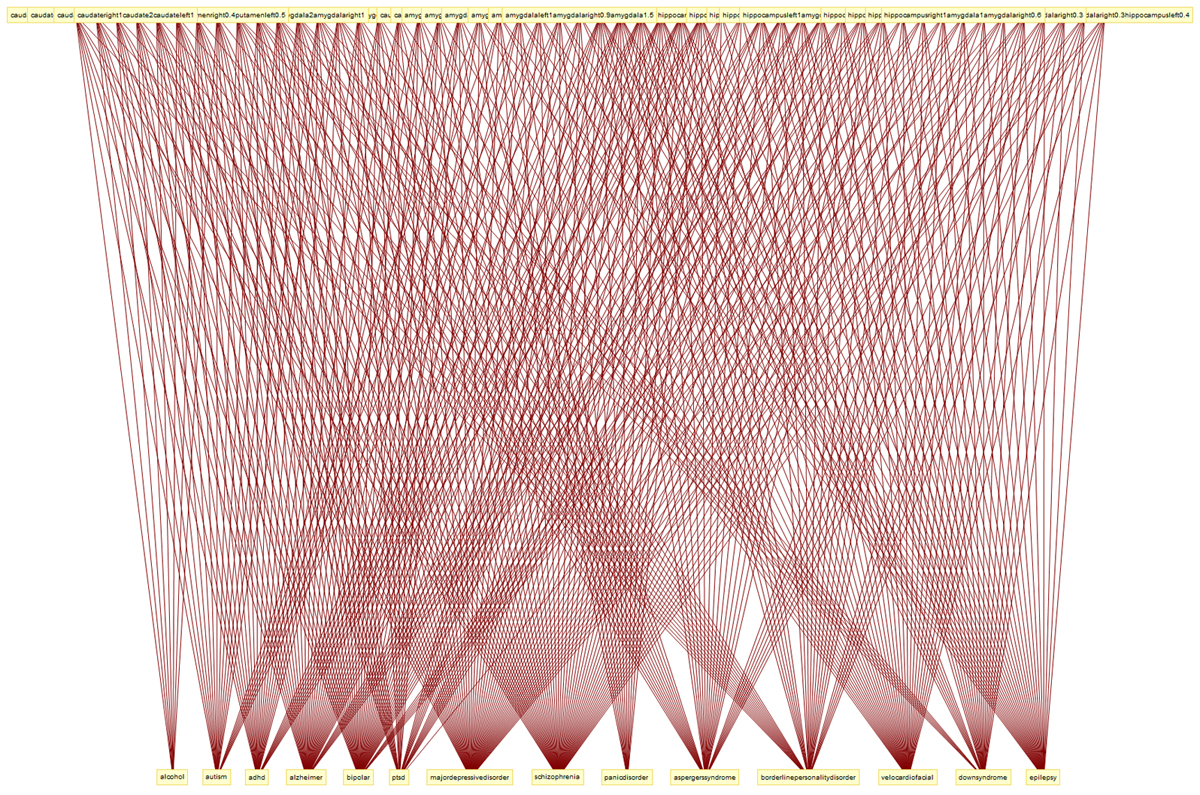
If we start with 21 well-defined disorders, phenotype each one with mathematical markers, and then mix all the markers together, we end up with a first approximation of what constitutes a disordered brain.
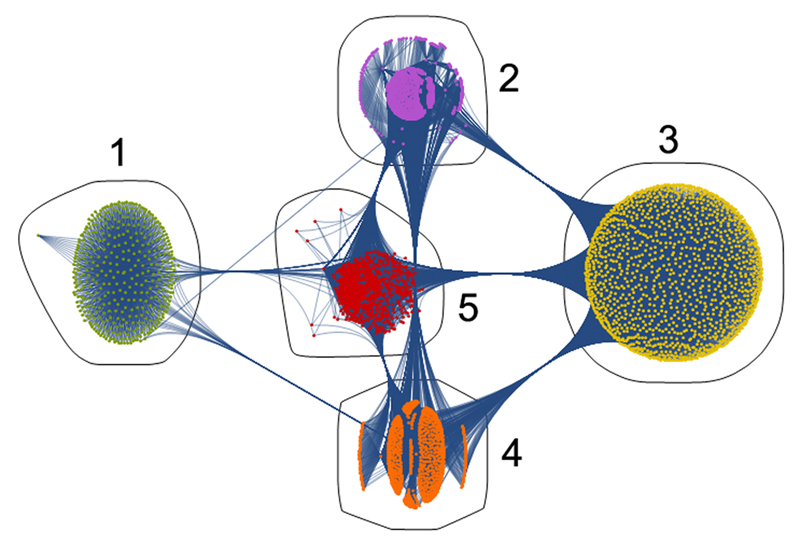
BEGIN THE UNFOLDING
From this mixture, communities of disorders will form according to the strength of their affinities.
This is how the clinical literature appears when expressed as a complexity (parts and connections) and designed to discover how disorders of the brain are related.
The first analysis finds five communities, …
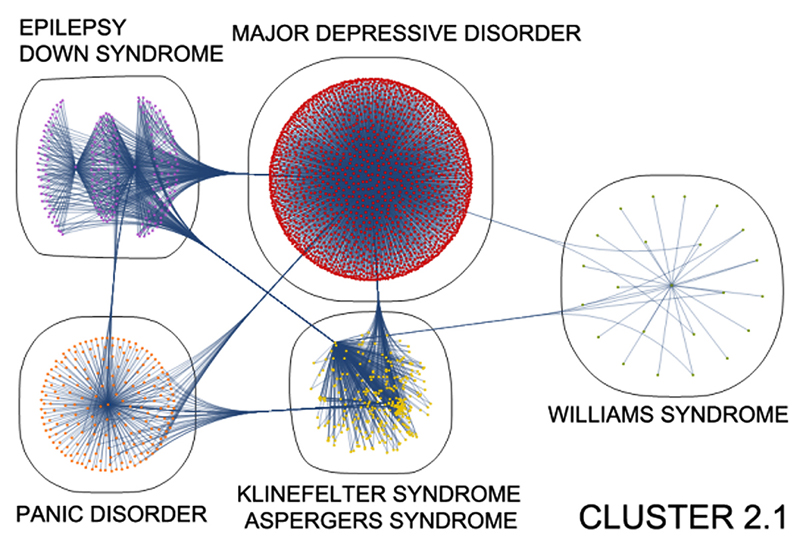
CONTINUE THE UNFOLDING
…which, in turn, yield progressively smaller communities…
FINISH THE UNFOLDING
…wherein only pairs of disorders remain.
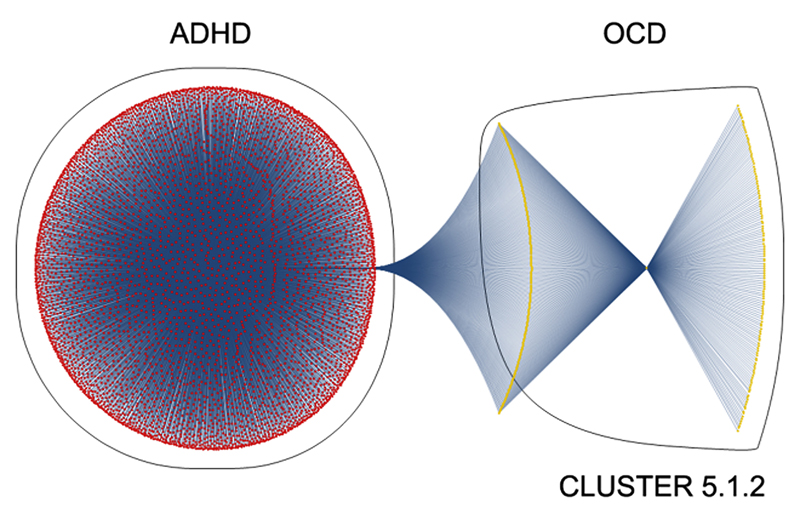
COMMUNITIES DEFINE BIG DATA GAMES
Finally, if we plot a small set of disorders with their markers, the magnitude of biological complexity as it exists in the human brain becomes apparent.

DIAGNOSIS AND PREDICTION
Diagnosis and prediction differ only by time.
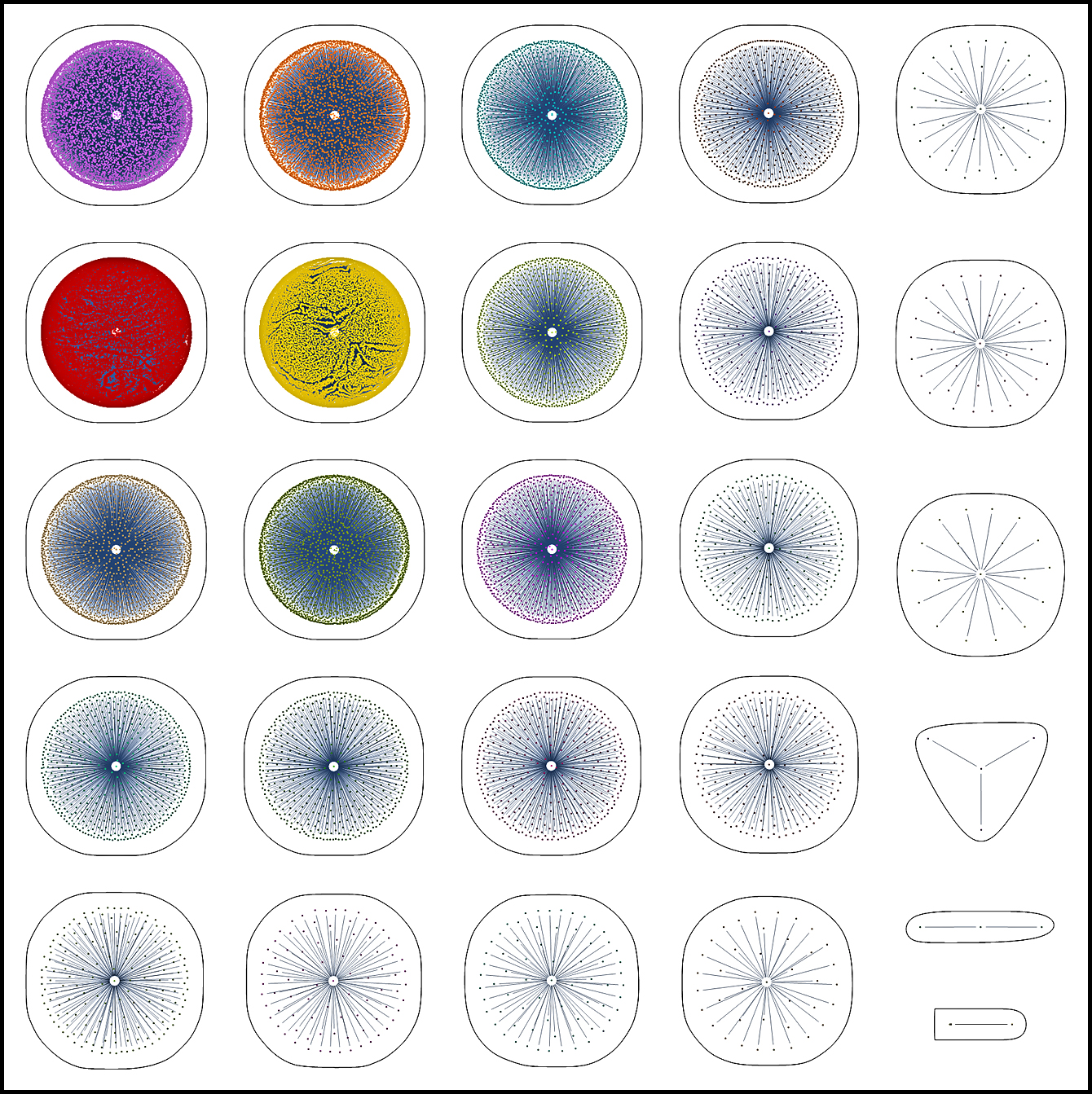
DATA CAGE
At the left is a data cage designed for the human brain. It includes a collection of twenty-six disorders – each of which exists in the figure as a central point surrounded by a set of unique mathematical markers. Notice that by eliminating the many connections that normally exist among such disorders, we effectively eliminate all the noise that would otherwise be coming from false positives. For convenience, the example is limited to 50,000 markers – out of 245,000.
This is what the clinical literature looks like when expressed as a complexity and converted into a diagnostic tool.
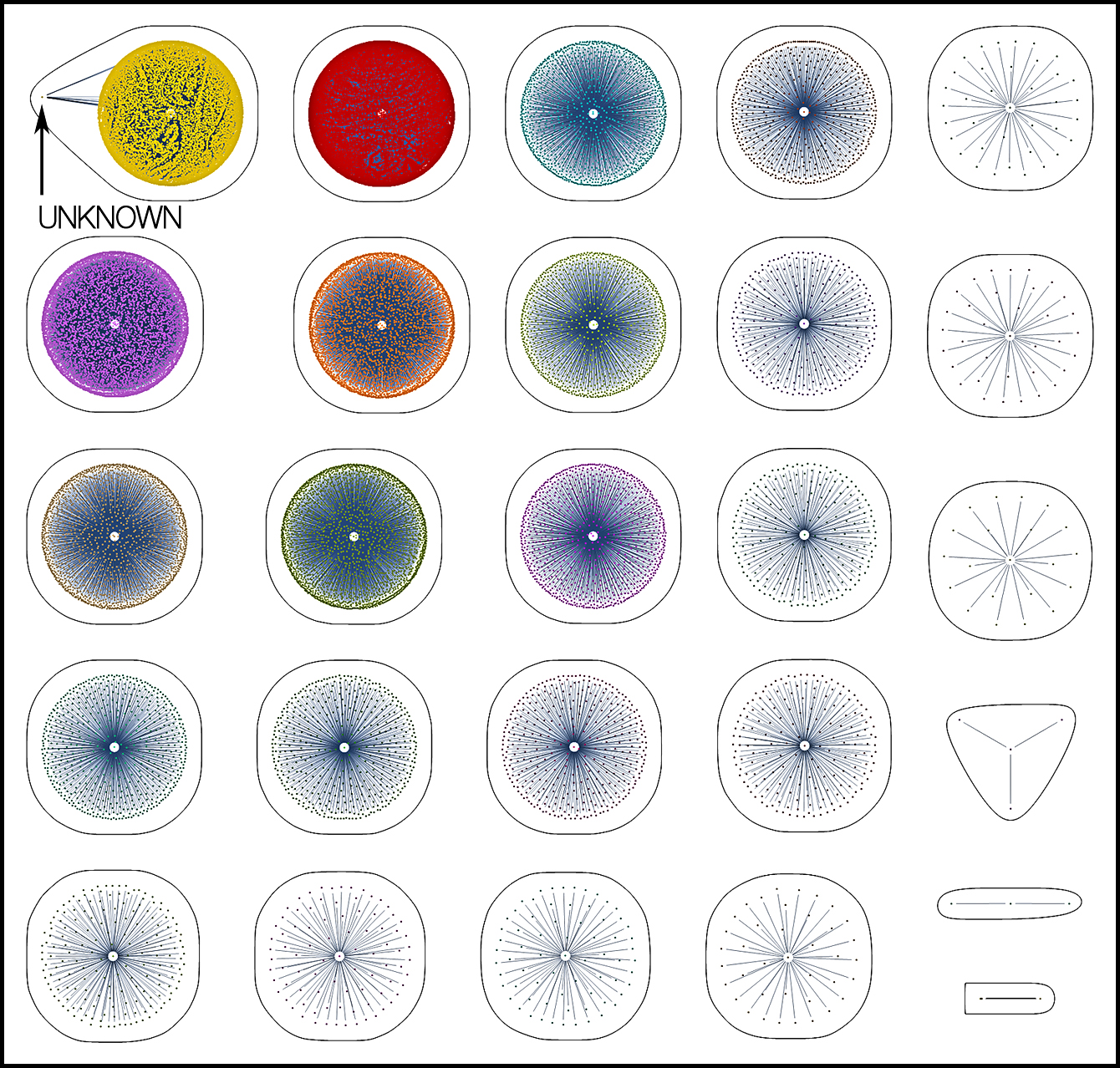
DATA CAGE IN ACTION
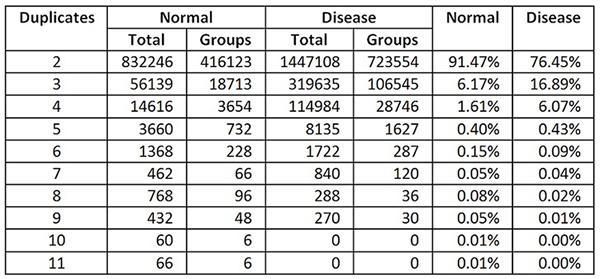
To illustrate the effectiveness of the data cage as a diagnostic tool, we can copy twenty markers from the same disorder, rename them as unknowns, and then plot the data a second time. The new plot shows that all the “unknowns” connect to a single disorder – the one from which they were originally copied (bipolar disorder). In effect, a data cage provides a quantitative standard to which unknowns can be compared – be they internal or external. In practice, the diagnostic test is surprisingly easy to run. It consists of adding unknowns to the database (245,000), identifying duplicates, and making the diagnosis (unknowns=knowns). It takes just a few minutes to run.
The point to take from the example is that our task in learning how to diagnose disorders as complex systems begins by first understanding the basic properties of the system in play. Since we now know that different disorders of the human brain often share similar mathematical markers, creating data cages to remove this overwhelming influx of false positives becomes a logical first step in preparing for a clinical diagnosis. We also know that large data sets derived from biology suffer grievously from a host of problems, which include experimental bias, biological variation, and false positives. The advantage of complexity theory is that it helps us to understand the root causes of these problems so that we can move confidently toward viable solutions. Think of it this way. If we know what’s broken, we can figure out how to fix it.

REPRODUCIBILITY TEST - REPORT 2016
Giving the job to biology…
TEST APPLIED TO THE LITERATURE
Most would agree that an ability to repeat the results of an experiment is fundamental to scientific discovery. Reproducibility, however, can be identified with precision or accuracy, the choice being left to the theory structure. Reductionist theory typically chooses precision (repeatability), whereas complexity theory prefers accuracy (correctness). To develop a test for reproducibility that can be applied to several published studies simultaneously, accuracy proved to be the best choice because the problem became a complex one. The test consisted of working backwards from global patterns (biology literature) to reproducible patterns (mathematical markers vs. connection ratios) to accuracy (biology). When applied to the MRI data of patients (67 studies), reproducibility was found to exist in surprisingly large amounts – as shown here and explained in the report (2016).

THE HOMOGENEITY POSTULATES - REPORT 2017
Test biochemistry first and then biology.
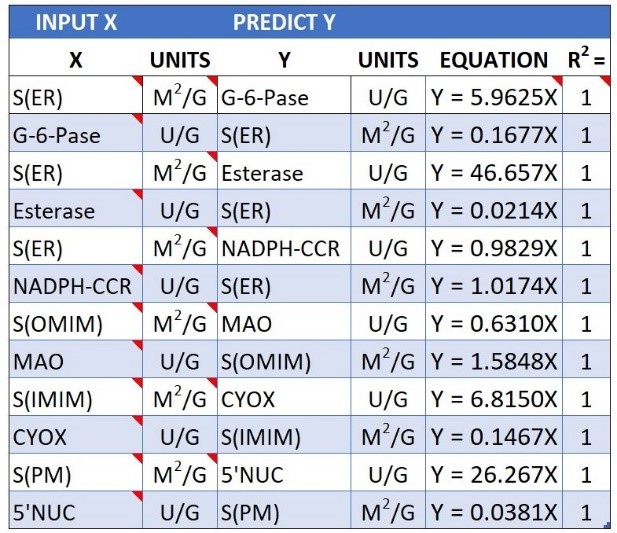
RULES STATED AS EQUATIONS
When morphological and biochemical data points fit a linear regression with an R2 = 1, the resulting equation identifies a biological rule with the ability to predict either structure or function. We can use such rules to play complexity games wherein we pose questions and biology predicts answers. In theory, this approach should allow us to reverse the direction of time so that we can discover where and how the rules are stored, coded, and read.

CHANGE - REPORT 2018
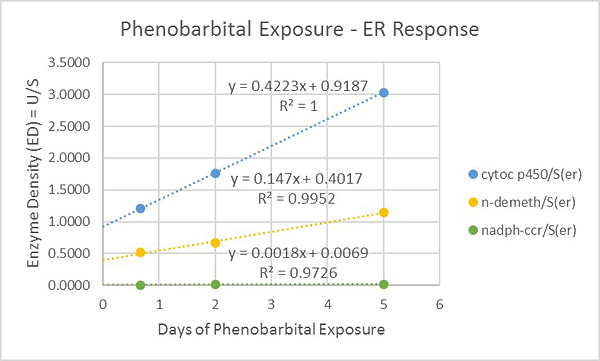
DETECTING CHANGES MATHEMATICALLY
When liver hepatocytes are exposed to the drug phenobarbital, they protect themselves by triggering the production of drug-metabolizing enzymes. To this end, the cells change by following specific recipes that redefine the relationship of structure and function in their ER membranes. The figure at the left shows enzyme densities (U/S – Units of enzyme activity per m2 of ER) for three of the marker enzymes contributing to this recipe. The rate constants, which are the slopes of the curves (delta y / delta x), identify the rate at which each enzyme is being added to the ER membrane.
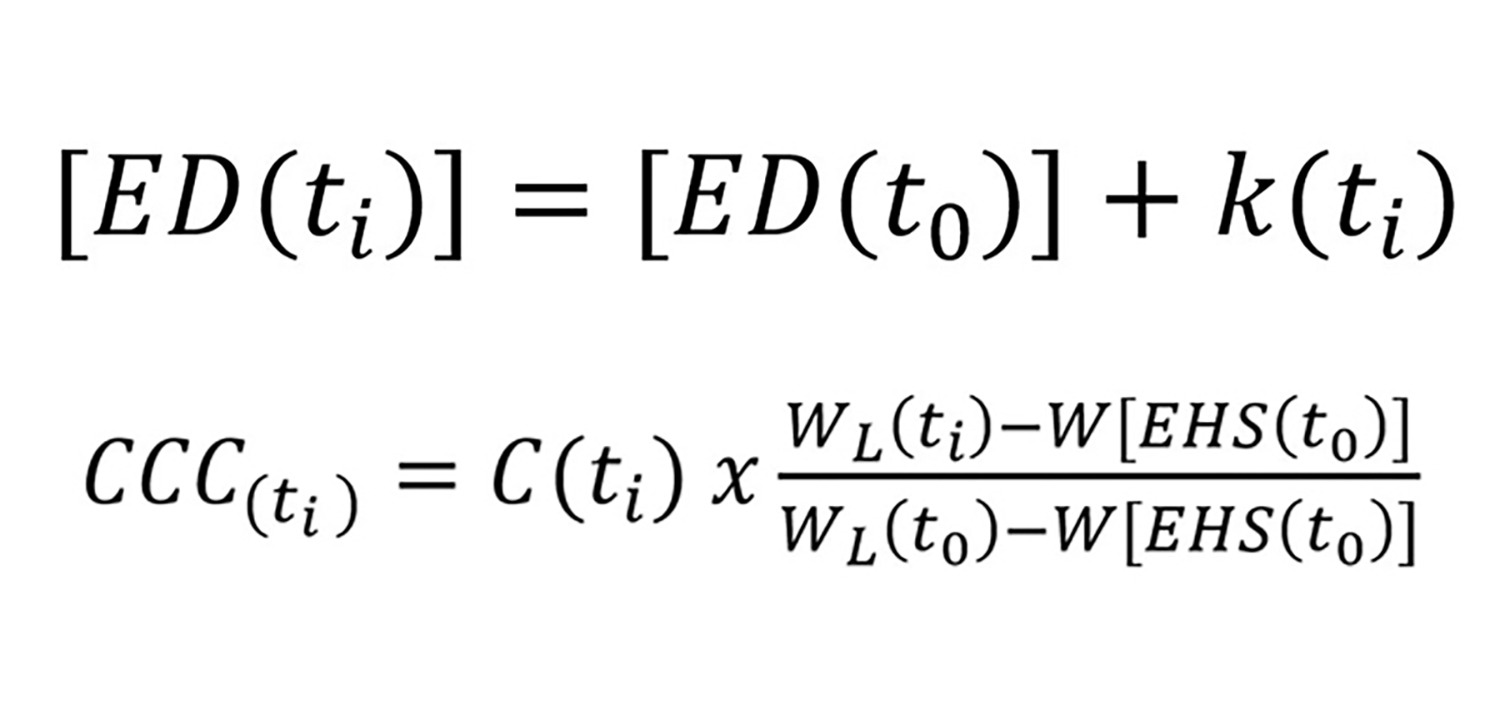
EQUATIONS AS SOLUTIONS
Two discrepancies occur repeatedly in the biomedical literature – a steadfast determination to use measures of individual parts to detect precision and accuracy (even though biology clearly prefers ratio-based rules) and the tendency to look for biological changes by comparing data coming from different numbers of cells. The first equation shown at the left uses membrane kinetics to improve precision and accuracy, whereas the second one keeps the number of cells constant throughout an experiment.
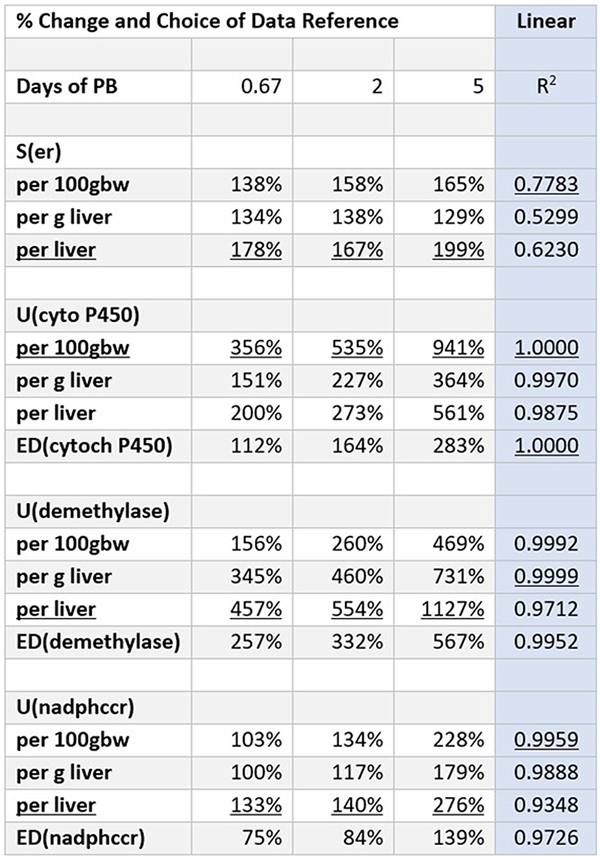
A SCORE CARD FOR CHANGE
Any given data set can provide a wide range of results, depending on one’s choice of reference. The table at the left serves as a score card for data references to illustrate this point, using data derived from Paper 1 (see Report). Best outcomes are underlined.
